证明（详细推导）

先把符号固定：设 $a=X_0,; b=X_1,; c=X_2,; d=X_3$。 题中已知第一步比较后有 $b>a$ 且 $c>d$（这里写成严格不等号；若只写非严格不等号，证明同理把“<”换成“$\le$”即可）。 定义第二步得到的四个数：

$$ X_4=\min(a,c),\quad X_5=\min(b,d),\quad X_6=\max(a,c),\quad X_7=\max(b,d). $$

下面逐条证明所需的不等式。

1. $X_4 \le X_6$（且当 $a\ne c$ 时为严格不等号）

因为 $X_4=\min(a,c)$ 且 $X_6=\max(a,c)$，对任意两数恒有 $\min(a,c)\le\max(a,c)$。若 $a\ne c$ 则 $\min(a,c)<\max(a,c)$。

2. $X_5 \le X_7$（且当 $b\ne d$ 时为严格不等号）

同上，$\min(b,d)\le\max(b,d)$，若 $b\ne d$ 则为严格不等号。

3. $X_4 < X_7$

证明链条：

• 因为 $X_4=\min(a,c)$，必有 $X_4\le a$（$\min$ 不大于任一元）。
• 由已知 $a<b$。
• 又 $X_7=\max(b,d)$，必有 $b\le X_7$。 把三句连起来得到

$$ X_4 \le a < b \le X_7 \quad\Longrightarrow\quad X_4 < X_7. $$

（中间的严格不等号 $a<b$ 保证了整体为严格不等号。）

4. $X_5 < X_6$

同理：

• $X_5=\min(b,d)$，所以 $X_5\le d$。
• 已知 $d<c$。
• $X_6=\max(a,c)$，所以 $c\le X_6$。 连起来：

$$ X_5 \le d < c \le X_6 \quad\Longrightarrow\quad X_5 < X_6. $$

把以上四条合并，就是

$$ X_4 \le X_6,\quad X_4 < X_7,\quad X_5 < X_6,\quad X_5 \le X_7. $$

如果再加上 $a\ne c$ 与 $b\ne d$（例如四个数两两互不相等）则所有“$\le$”都变为“$<$”，即正好得到四个严格不等式：

$$ X_4 < X_6,\quad X_4 < X_7,\quad X_5 < X_6,\quad X_5 < X_7. $$

直观解释（帮助记忆）

• 第一步使得每对内部是升序：$a<b$ 和 $d<c$。
• 第二步把“外侧”的 $a,c$ 做一次 min/max，把“内侧”的 $b,d$ 也做一次 min/max。由于 $a$ 已经小于 $b$ 而 $d$ 已经小于 $c$，所以任一左边的 min 不可能超过任一右边的 max——这就是“左侧都小于右侧”的直观原因。

举例验证

取 $a=1,; b=3,; c=4,; d=2$（满足 $b>a,; c>d$）： $X_4=\min(1,4)=1,; X_5=\min(3,2)=2,; X_6=\max(1,4)=4,; X_7=\max(3,2)=3$。 确实有 $1<4,;1<3,;2<4,;2<3$。

我把 4 个数上的观察提升为一个归纳 / 递归证明（也就是经典的 bitonic merge 证明）。目标是把思路讲清楚、严格，但尽量直观易懂。下面给出两个部分：

• 先说明关键引理（长度为 $2^k$ 的“双条/bitonic”序列，在把每对相距 $2^{k-1}$ 的元素做一次 min/max 后，左半段的任意元素 ≤ 右半段的任意元素；且左右两段仍然是 bitonic），
• 再用归纳把 $4$ 的结论推广到 $8$、$16$、…… 任意 $2^n$。

我把符号统一一下，便于阅读。

记号与假设

令长度为 $2^n$ 的序列为

$$ S=(x_0,x_1,\dots,x_{2^n-1}). $$

我们说 $S$ 是一个 bitonic（双条）序列且“峰”在中间，意思是：把序列在中间切成两半

$$ A=(x_0,\dots,x_{m-1}),\qquad B=(x_m,\dots,x_{2m-1}),\quad m=2^{n-1}, $$

满足 $A$ 是单调非减（或非增，取决于约定）到接近中心，$B$ 是在中心向外单调相反方向；更简单的约定（与题目一致）：我们已把序列旋转/安排好，使得 $x_{m-1}$ 和 $x_m$ 是序列中最大的两个元素（也就是“峰”确实落在两半的边界处）。（八个数的例子就是 $m=4$，且 $x_3,x_4$ 为最大两个，$x_0,x_7$ 为最小两个的情形。）

现在对每个 $i=0,\dots,m-1$ 做一次成对比较与置换：

$$ y_i=\min(x_i,x_{i+m}),\qquad y_{i+m}=\max(x_i,x_{i+m}). $$

得到新序列 $Y=(y_0,\dots,y_{2m-1})$。要证明的关键结论是：

引理（核心）：对于任意 bitonic 序列 $S$（峰在中间），做上面的 $m$ 个成对 min/max 后，

1. $y_i \le y_{j+m}$ 对任意 $0\le i,j<m$ 都成立（即左半段的任意元素 ≤ 右半段的任意元素）；
2. 左半段 $Y_L=(y_0,\dots,y_{m-1})$ 与右半段 $Y_R=(y_m,\dots,y_{2m-1})$ 都仍然是 bitonic（并且长度均为 $m$），因此可以递归继续相同操作。

下面把这个引理证明清楚；然后给出归纳过程。

引理证明

先给出直观框架：对每对 $(x_i,x_{i+m})$ 取最小的放左、最大的放右，直觉上左边集合由一堆“较小”值组成，右边由“较大”值组成；要把“任意左 ≤ 任意右”变成形式化，常用的路线是反设法（反证）。

证明（反证）：假设引理 1 不成立，则存在 $i,j\in{0,\dots,m-1}$ 使得

$$ y_i > y_{j+m}. $$

按定义 $y_i=\min(x_i,x_{i+m})$ 且 $y_{j+m}=\max(x_j,x_{j+m})$。所以

$$ \min(x_i,x_{i+m}) > \max(x_j,x_{j+m}). $$

这意味着四个原始数满足

$$ x_i > x_j,\quad x_i > x_{j+m},\quad x_{i+m} > x_j,\quad x_{i+m} > x_{j+m}. $$

即第 $i$ 对的两个数都严格大于第 $j$ 对的两个数。

考虑它们在原序列中的位置：

• $x_i$ 与 $x_{i+m}$ 分别位于两半的对应位置：一个在左半（索引 $i$），一个在右半（索引 $i+m$）；同理第 $j$ 对。
• 由于我们假设“峰”在两半的边界处，左半 $A$ 的元素从左到右是先上升到 $x_{m-1}$（或至少不超过 $x_{m-1}$），而右半 $B$ 的元素从 $x_m$ 向右是先下降（或至少不超过 $x_m$）。换言之，左半的右端 $x_{m-1}$ 与右半的左端 $x_m$ 是两个全局最大的值（并且没有其它值能超过它们），这给出严格的顺序约束。

现在从两对之间的相对大小出发，会得到与 bitonic 单调性冲突：

• 若 $i\le j$，那么 $x_i$ 在左半更靠左或同列，按左半（到中心）是非减的性质，$x_i \le x_j$ 应该成立（或者至少不可能都严格大于）。但我们已经从假设得到 $x_i > x_j$，矛盾。
• 若 $i>j$，则 $i+m > j+m$（对应右半的位置更靠右）。而右半是从中心向右“非增”的（或单调相反方向），因此在右半靠右的位置的元素不可能严格大于更靠左的位置元素：即 $x_{i+m} \le x_{j+m}$，但假设给出 $x_{i+m} > x_{j+m}$，同样矛盾。

更直观一点：两个对应索引 $i$ 与 $j$ 在左右两端的位置关系（左半按从边到中增长、右半按从中到边下降）决定了如果 $i\le j$ 则左半第 $i$ 个元素不能大于左半第 $j$ 个元素；如果 $i>j$ 则右半第 $i$ 个元素不能大于右半第 $j$ 个元素。无论哪种情况，都与“第 $i$ 对的两个数都大于第 $j$ 对的两个数”矛盾。于是反设不成立，证明了

$$ \forall i,j:\quad y_i \le y_{j+m}. $$

因此（结论 1）成立：左任意 ≤ 右任意。

接下来要说明左右各自仍为 bitonic（结论 2）。这一点可以直接从原序列的单调片段结构看出：

• 原来左半 $A=(x_0,\dots,x_{m-1})$ 是从左向中“上升”（或至少不减），右半 $B=(x_m,\dots,x_{2m-1})$ 是从中向右“下降”。
• 对每个对应对取 $\min$ 放入左半（得到 $Y_L$），因为左边的元素在索引上从左到右趋近峰值、而右边的对应元素从峰向外减小，两个数做 $\min$ 后，$Y_L$ 的总体形状仍然保持“先增后减”的结构（或者更直接地：可以逐对检查 $y_i$ 与 $y_{i+1}$ 的关系，证明 $Y_L$ 其实是 bitonic）。同理对 $\max$ 放入右半，得到的 $Y_R$ 也仍为 bitonic。（这是 bitonic merge 的标准性质；若需要我可以把对相邻索引的单调关系写成逐项不等式证明。）

综上，引理成立。

归纳主定理（把 4 → 8 → … 推开）

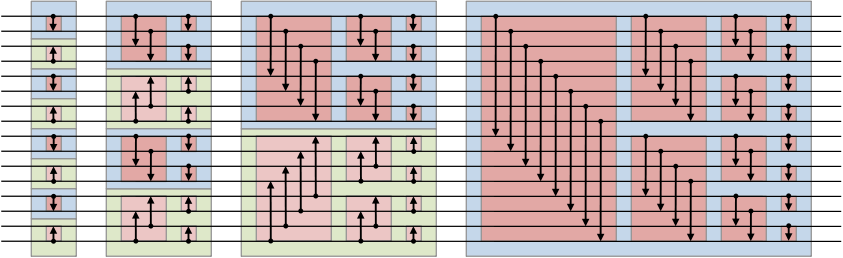
现在用归纳法说明：对任意 $n$，设长度为 $2^n$ 的 bitonic 序列（峰在中间），执行以下算法可以把整个序列合并成一个“左全小于右全大”的分割，并可递归完成排序：

算法（bitonic merge 的一层）：

1. 令 $m=2^{n-1}$。对每个 $i=0,\dots,m-1$ 做 $(x_i,x_{i+m})$ 的 compare-exchange（把小的放左，大的放右）。
2. 得到左右两段 $Y_L,Y_R$，它们各自为长度 $m$ 的 bitonic 序列（由引理），且任意 $y\in Y_L,; z\in Y_R$ 有 $y\le z$。
3. 若 $m>1$，则对 $Y_L$ 和 $Y_R$ 递归执行同样的操作（即把每段继续按相同模式配对比较）。

归纳基础：当 $n=1$（长度 2）时，配对 min/max 后显然左 ≤ 右；当 $n=2$（长度 4）就是最开始给出的详细证明，我们也已验证。

归纳步骤：假设对长度 $2^n$ 的任何 bitonic 序列该算法成立（引理 + 递归能把它拆成左右且左全小于右），现在考虑长度 $2^{n+1}$。对距离 $2^n$ 做一次成对比较（step 1），由引理得到左右两段每段都是长度 $2^n$ 的 bitonic 且左全小于右。由归纳假设，对左右两段各自继续递归处理，最终能把每段正确合并（即内部达成左小于右），并且由于整段左任意 ≤ 右任意，最终整个 $2^{n+1}$ 长度的序列也按“左半所有 ≤ 右半所有”分割成立。这就是完整的归纳证明。

回到 8 个数的例子

把上面专门写成 $n=3$ 的情形：$2^3=8$，$m=4$。 $x_3,x_4$ 为两个最大（峰在中间），那正好满足引理的假设。对 $i=0,1,2,3$ 分别把 $(x_i,x_{i+4})$ 变为 $\min$ 放左 $\max$ 放右，得到的左四个 $y_0..y_3$ 与右四个 $y_4..y_7$ 满足：任意左 ≤ 任意右，且左右各自仍是 bitonic。然后对左四个和右四个再做同样的处理（这时就回到最早处理 4 个数的情形），最终得到每半内部也完成“左小于右”的性质，整个 8 个数就被正确合并。

直观总结

• 对任意长度为 $2^n$ 的 bitonic 序列（峰放在两半的边界），把每对相距 $2^{n-1}$ 的元素做一次 compare-exchange（min 左 max 右），可以一次性把序列分成左半全 ≤ 右半全；
• 之后对左右两半递归做同样操作，直到长度为 1，就得到了完全有序的合并（这就是 bitonic merge network 的工作原理）。
• 最开始的 4 元例子就是 $n=2$ 的特例；8 元就是 $n=3$ 的一次递归展开——完全由上面的引理 + 归纳推导出来。

关键点确实在于 “成对取 min/max 后左右两半仍然是 bitonic” 这一性质为什么成立。下面把证明写得尽量清楚且可验算（含 8 个数的具体示例）。

设定（同前）

长度为 $2m$（比如 $m=4$）的序列

$$ X=(x_0,x_1,\dots,x_{2m-1}) $$

假设这是一个“峰在中间”的 bitonic 序列（和例子一致）：

$$ x_0\le x_1\le\cdots\le x_{m-1},\qquad x_m\ge x_{m+1}\ge\cdots\ge x_{2m-1}. $$

也就是说左半段 $A=(x_0,\dots,x_{m-1})$ 从左向中非减，右半段 $B=(x_m,\dots,x_{2m-1})$ 从中向右非增。

进行一轮跨半长的比较-交换（distance $m$）：

$$ y_i=\min(x_i,x_{i+m}),\qquad y_{i+m}=\max(x_i,x_{i+m}),\quad i=0,\dots,m-1. $$

得到新序列 $Y=(y_0,\dots,y_{2m-1})$。问题是：为什么 $Y_L=(y_0,\dots,y_{m-1})$ 与 $Y_R=(y_m,\dots,y_{2m-1})$ 仍然是 bitonic 呢？（如果不成立，接下来的 span 为 $m/2$ 的合并确实会“失效”。）

证明要点（核心观测：差函数单调）

定义两个函数

$$ f(i)=x_i,\qquad g(i)=x_{i+m}\quad (i=0,\dots,m-1), $$

以及差函数

$$ h(i)=f(i)-g(i)=x_i-x_{i+m}. $$

注意到：

• 因为 $f(i)=x_i$ 在 $i$ 增加时非减（左半段非减），所以 $f(i+1)-f(i)\ge0$；
• 因为 $g(i)=x_{i+m}$ 在 $i$ 增加时对应索引 $i+m$ 增加，而右半段是非增，所以 $g(i+1)-g(i)=x_{i+1+m}-x_{i+m}\le0$。

于是

$$ h(i+1)-h(i)=(f(i+1)-f(i))-(g(i+1)-g(i))\ge 0 - ( \le 0 ) \ge 0. $$

所以 $h(i)$ 随 $i$ 非减。这一步是关键：它告诉我们 $h(i)$ 只会由小到大、最多有一次从负变到正（也可能恰为 0 若相等）。

因此存在一个分界索引 $k$（可以取为最大满足 $h(k)\le0$ 的 $k$），使得

• 对 $i\le k$：$h(i)\le0\Rightarrow f(i)\le g(i)\Rightarrow y_i=f(i)$（左边取小的是左半的原值）；
• 对 $i>k$：$h(i)\ge0\Rightarrow f(i)\ge g(i)\Rightarrow y_i=g(i)$（左边取小的是右半的原值）。

也就是说

$$ Y_L=(y_0,\dots,y_{m-1})=(,f(0),f(1),\dots,f(k);,; g(k+1),g(k+2),\dots,g(m-1),). $$

前半段是 $f(0..k)$ —— 非减（因为是左半原本的前缀）；后半段是 $g(k+1..m-1)$ —— 非增（因为是右半原本的一个后缀，右半是从中向右非增）。因此 $Y_L$ 是“先非减后非增”的串 —— 正式上就是一个 bitonic 序列（先上升后下降，最多只有一次转折）。

对右半 $Y_R$ 同理：

• 对 $i\le k$ 有 $y_{i+m}=z_i=g(i)$（取较大的是原右半的值），
• 对 $i>k$ 有 $y_{i+m}=z_i=f(i)$。

即

$$ Y_R=(,g(0),g(1),\dots,g(k);,; f(k+1),\dots,f(m-1),). $$

这是一段“先非增（g 的前缀）再非减（f 的后缀）”的串。虽然形状是“先降再升”（中间是谷），但这仍然是一个 bitonic 序列（bitonic 的宽义是“至多一次单调方向变化”——可视作把序列旋转后变为先升后降的形式）。

结论

• 我们 并没有 在第一步后“只保证左边元素都比右边小”而丢失左右段的结构。实际上通过差函数 $h(i)$ 的单调性可以严格证明：左半和右半各自仍然是 bitonic（左半是先增后减，右半是先减后增 —— 两者都只有一个单调性变化点）。
• 因为两半都是 bitonic，所以对每一半再进行跨度为 $m/2$ 的 compare-exchange（即递归地做相同操作）是合法且有效的 —— 这正是 bitonic-merge 的核心：每次把跨半的比较做完后，左右两半仍保持可递归处理的 bitonic 结构，最终能完成合并/排序。

一个具体的 8 元例子（帮助直观理解）

取

$$ x=(1,3,5,9,;10,7,4,2) $$

左半 $1\le3\le5\le9$，右半 $10\ge7\ge4\ge2$。跨半比较（距离 4）：

• 对应对：$(1,10),(3,7),(5,4),(9,2)$
• 得到 $Y_L=\big(\min(1,10),\min(3,7),\min(5,4),\min(9,2)\big)=(1,3,4,2)$ —— 先 1≤3≤4，然后 4≥2（先增后降，bitonic）。
• 得到 $Y_R=\big(\max(1,10),\max(3,7),\max(5,4),\max(9,2)\big)=(10,7,5,9)$ —— 10≥7≥5 然后 5≤9（先降后升，也是“单次变向”的序列，属于 bitonic 的一种形式）。

于是对每半再用跨度 2 的 compare-exchange 即可继续递归，最终完成合并。